Poker básico. Calcular odds usando la "regla del 4"

Anónimo (gran lector de blogs) preguntaba en una entrada anterior (Vamos a contar OUTs) dos cosas:

Q: "No sé si este blog sigue abierto"
A: Este blog sigue abierto. Habrá nuevos contenidos cuando elaboremos más material.

Q: "en el metodo abreviado ese para el calculo [de odds], me podrias decir de donde viene el 8 ese"
A: Se trata de la famosa "regla del 4"

Calcular ODDs en el TURN usando la regal del 4

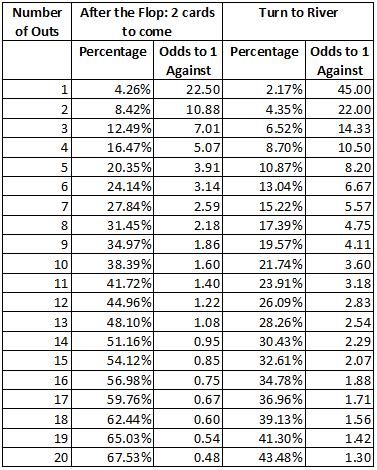
Todos conocemos las tablas de ODDs como la que adjunto al final de esta entrada. Pues bien para calcular mentalmente los odds en el turn solo hay que aplicar la "famosa" regla del cuatro.

Si el número de OUTs es menor de 8:

ODDs (%) = OUTs * 4                    [1]

Si el número de OUTs es mayor de 8:

ODDs (%) = OUTs * 4 - (OUTs - 8)       [2]

Se puede comprobar en la tabla que la fórmula [1] funciona cuando el número de OUTs es menor de 8. Cuando es mayor se puede aplicar la fórmula [2] como hicimos en la entrada de la polémica: Vamos a contar OUTs




Background matemático

¿por qué funciona la regla del 4? La probabilidad de 1 OUT en el TURN es 4,25%
4,25% = 1 - (46/47) * (45/46)
Entonces la probabilidad de varios OUTs se puede aproximar multiplicando el número de OUTs por 4% que es, aproximadamente, la probabilidad de un OUT. La corrección cuando el número de OUTs es mayor de 8 es necesaria porque cuando aumenta el número de OUTs aumenta la probabilidad de que coincida uno de los OUTs en el TURN y otro en el RIVER.

La regla del 2

La regla del 2 es muy simple. Para calcular los ODDs en el RIVER sólo hay que multiplicar el número de OUTs por 2. Si se quiere mayor precisión se debería multiplicar por 2,17% que es la probabilidad de que salga un OUT en el RIVER:

2,17% = 1/46

La regla del 2 no necesita ninguna corrección como se puede comprobar en la tabla.

Arthur Benjamin. "Matemago"

Arthur Benjamin habla sobre el posicionamiento del Cálculo (antiguo, aburrido, continuo) frente a la Estadísticas (moderno, divertido, discreto). Bueno, es una opinión.

Poker básico con ejemplos. Vamos a contar OUTs

Contar OUTs es básico, muy básico. Observe, el lector, la siguiente mano:

No Limit Holdem Tournament
$5.00+$0.20
10 players
Converted at weaktight.com

Blinds: 15/30

Pre-flop: (45, 10 players) Hero is BB

1 fold, Dominus666 (UTG+2) raises to 360, 7 folds, Hero calls 330

> Las ciegas están en 15/30. Estamos en la ciega grande, y Dominus desde UTG+2 sube 360 (normal, tiene QQ). Con KQs vamos a defender nuestra ciega.

Main Pot (735)

Flop: (735, 2 players)

Hero checks, Dominus666 goes all-in 1,060,

Flop interesante, Dominus mete la caja. Estamos en las primeras manos del S&G, no tenemos nada ("K high") pero tenemos algunos OUTs.

¿cuántos OUTs tenemos?
1. vamos a suponer que el rival tiene AA, AKs, AKo o KK. En el "peor" de los casos podría tener JJ y haber pillado set máximo en el flop.
2. en todos los casos anteriores las siguientes cartas nos dan jugada ganadora:
- todos los corazones: 9
- todos los ases (excepto el de corazones que ya está contado): 3
- todos los nueves: 3
3. A esto sumamos los reyes que nos darían una pareja superior que la del rival: 3
4. En total, tenemos 18 outs, quedan 47 cartas ocultas y aún tienen que salir 2 cartas. Esto es, aproximadamente, un 62%.

Método abreviado: 18 (outs) * 4 (turn+river) - 10 (18 - 8) = 62%

Es decir, hay más del 50% de posiblidad de completar la jugada. INSTA-CALL

Hero calls 1,060

Main Pot (2,855)
Turn: (2,855, 2 players)

El TURN falló

Main Pot (2,855)

River: (2,855, 3 players)

El RIVER "acertó"

Main Pot (2,855)
Final Pot: 2,855
Hero shows:
Dominus666 shows:

Escalera real de color, jugada máxima y bote ganado

En este caso no hay que calcular los odds del bote porque nuestra probabilidad de ganar (equity) es mayor de 0,5. Como tenemos más probabilidad de ganar que de perder cualquier bote nos va a dar un EV positivo.