Dejé de jugar
Dejé de jugar a Poker. Esa es la razón por la que no escribo aquí y por la que no aparezco por allí. Ahora dedico el tiempo libre a escribir, jugar Backgammon, montar estanterías de IKEA y ver la tele. No hay más motivos (ni menos).
Probabilidad: ¿qué probabilidad hay de que pase "esto"?
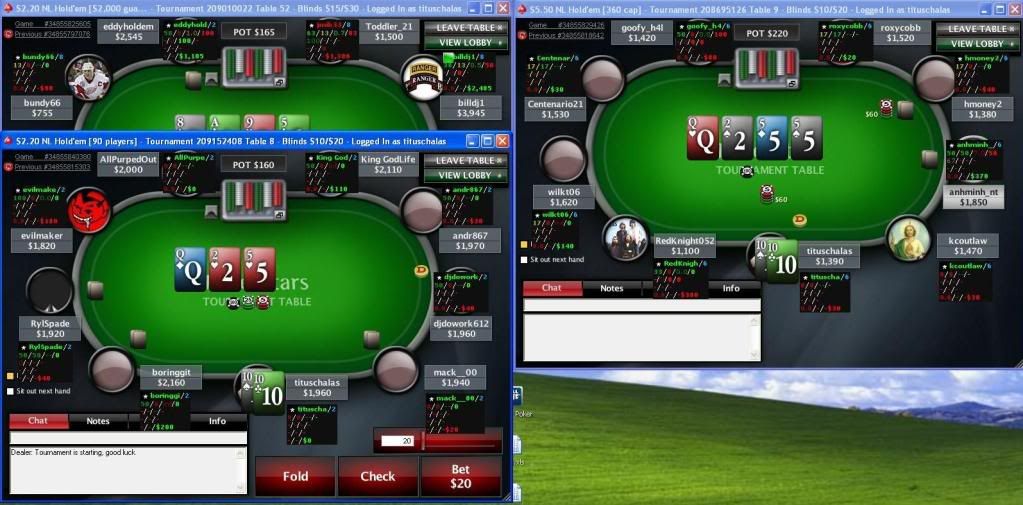
Sacado de Poker-red: Prueba irrefutable, el software de Pokerstars no es aleatorio
WTF (que significa "What The Fuck")! Jugando en dos mesas simultáneas sale la misma jugada: las mismas dos cartas de mano y el mismo flop. Esto está amañado!
Tranquilidad, que no cunda el pánico. Vamos a analizar la jugada por partes.
1. No es la misma jugada.
Los dos flops son diferentes:
Flop 1:



Flop 2:



Observe el lector que las seis cartas son diferentes. No se repite ninguna.
2. Ahora el cálculo probabilístico
2a. ¿qué probabilidad tengo de que en la segunda mesa me salga la misma mano que en la primera?
Fácil. 1/52 es la probabilidad de que la primera carta coincida y 1/52*1/51 la probabilidad de que coincida la segunda habiendo coincidido la primera. Total: 1/2642. Pues no es tan difícil que te coincida la misma mano en dos mesas a la vez.
2b. ¿qué probabilidad hay de que coincida en la segunda mesa el mismo flop que en la primera sin tener en cuenta el color?
Esto es importante. A veces vemos en una mesa ATo y en otra mesa ATo y decimos, ¡es la misma jugada! Bueno, es equivalente pero si los palos no coinciden no es exactamente la misma jugada.
En nuestro caso, la probabilidad que buscamos es:
4/50 en la primera carta del flop (hay 4 Qs y 50 cartas ocultas)
4/49 en la segunda
4/48 en la tercera
En total, hay una probabilidad entre 2.436.525 de que esto ocurra. No es fácil pero no es, tampoco, para ponerse así.
10 Razones por las cuales kobe_jnk nunca será un gran ganador en el poker.
Este post de "kobe_jnk" en Poker-red es de lo mejor que he leído sobre poker últimamente. Indico sólo los titulares (y mis comentarios en cursiva), para el contenido completo podeís ir a la fuente.
"10 razones por las que nunca sere un gran ganador en el poker"
1. Porque soy un vago
Yo no soy un vago pero como al poker le dedico una hora al día, necesito un año para hacer lo que otros hacen en un mes.
2. Porque no selecciono las mesas
Yo tampoco selecciono las mesas. Juego Sits y MTT y juego el primero que esté en la lista. Ni leo el nombre de los jugadores registrados.
3. Porque me afectan las perdidas y las ganancias
No me afectan ni las perdidas ni las ganancias porque juego muy poco y en mesas "baratas".
4. Porque odio las matematicas
A mí me encantan las matemáticas.
5. Porque no soy ambicioso
Efectivamente, la ambición ayuda a jugar mejor. Cuando no tienes ambición prefieres jugar a estudiar (por ejemplo)
6. porque me supervaloro y me infravaloro demasiado amenudo.
Yo más. A veces me sobrevaloro como el que más y otras veces me pongo en modo "superviviente" y, lógicamente, acabo palmando.
7. Porque me cuesta asimilar lo estudiado
A mí me cuesta aplicar lo que estudio. Por ejemplo, sigo jugando manos como A6s y KTo.
8. Porque me cuesta mucho leer las jugada
A mí me cuesta jugar algunas jugadas. Entro en botes sin ningún objetivo con manos que no sé jugar. No sé, por ejemplo, jugar una segunda pareja y, lógicamente, no tengo una estrategia concreta para este caso.
9. Porque no me adapto a la mesa
Yo sólo me adapto a las mesas llenas de fishes, loose-pasivos ;)
10. Porque no peto los niveles
Yo juego siempre el mismo nivel
"10 razones por las que nunca sere un gran ganador en el poker"
1. Porque soy un vago
Yo no soy un vago pero como al poker le dedico una hora al día, necesito un año para hacer lo que otros hacen en un mes.
2. Porque no selecciono las mesas
Yo tampoco selecciono las mesas. Juego Sits y MTT y juego el primero que esté en la lista. Ni leo el nombre de los jugadores registrados.
3. Porque me afectan las perdidas y las ganancias
No me afectan ni las perdidas ni las ganancias porque juego muy poco y en mesas "baratas".
4. Porque odio las matematicas
A mí me encantan las matemáticas.
5. Porque no soy ambicioso
Efectivamente, la ambición ayuda a jugar mejor. Cuando no tienes ambición prefieres jugar a estudiar (por ejemplo)
6. porque me supervaloro y me infravaloro demasiado amenudo.
Yo más. A veces me sobrevaloro como el que más y otras veces me pongo en modo "superviviente" y, lógicamente, acabo palmando.
7. Porque me cuesta asimilar lo estudiado
A mí me cuesta aplicar lo que estudio. Por ejemplo, sigo jugando manos como A6s y KTo.
8. Porque me cuesta mucho leer las jugada
A mí me cuesta jugar algunas jugadas. Entro en botes sin ningún objetivo con manos que no sé jugar. No sé, por ejemplo, jugar una segunda pareja y, lógicamente, no tengo una estrategia concreta para este caso.
9. Porque no me adapto a la mesa
Yo sólo me adapto a las mesas llenas de fishes, loose-pasivos ;)
10. Porque no peto los niveles
Yo juego siempre el mismo nivel
Backgammon

Fuente: Danheller.com
Encuentro en Pokerviu una entrada sobre este juego: + que Poker : Backgammon. En el artículo hay dos vídeos, el primero muestra a "nuestro amigo" Gus Hansen explicando las reglas básicas del juego y el segundo es una partida del propio Gus con otro tipo. Realmente espectacular el segundo vídeo; muy recomendable.
Aprendimos a jugar Backgammon después de visitar Turquía. En todo el Mediterráneo oriental (Turquía, Egipto, Grecia) es muy habitual ver a la gente jugando a este juego. Recuerdo cómo jugábamos en la cubierta de los ferrys que nos llevaban de una isla a otra del Egeo o como veíamos atardecer mientras jugábamos en la cubierto del crucero que atravesaba Egipto por el Nilo. Actualmente, sólo juego al GNU Backgammon cuando no tengo conexión y no puedo jugar Poker.
a long way down
A long way down, de Nick Hornby es un libro estupendo que, además, se lee fácil en inglés. Pues eso, a long way down.


HHJReader 2.0. Descarga gratis
El proyecto HHJReader (estupendo programa) está parado.
Labot parece que tiene mucho trabajo y ya no tiene tiempo para ayudarme con ello. Mi intención de aprender a programar en Java sólo me dio para el básico "public class HelloWorld".
Así que, hasta que convenza a otro programador o aprenda a programar, he aparcado el proyecto.
He subido la última versión que desarrollamos. El enlace está al final de este mensaje.
Recordad las limitaciones de HHJReader 2.0:
- sólo "lee" ficheros de manos de PokerStars en Inglés.
- no puede abrir varios ficheros simultáneamente, pero sí puedes ejecutar el programa varias veces.
Si queréis saber qué es capaz de hacer este programa, podéis consultar las entradas de este blog sobre HHJReader: http://isabella70.blogspot.com/search?q=hhjreader
Para descargarlo podéis usar el siguiente enlace (no he encontrado ningún hosting mejor): http://www.filefactory.com/file/a2ga953/n/HHJReader_v2-0_zip
El programa se suministra "tal cual", no garantizamos ningún tipo de soporte ni ayuda.
Labot parece que tiene mucho trabajo y ya no tiene tiempo para ayudarme con ello. Mi intención de aprender a programar en Java sólo me dio para el básico "public class HelloWorld".
Así que, hasta que convenza a otro programador o aprenda a programar, he aparcado el proyecto.
He subido la última versión que desarrollamos. El enlace está al final de este mensaje.
Recordad las limitaciones de HHJReader 2.0:
- sólo "lee" ficheros de manos de PokerStars en Inglés.
- no puede abrir varios ficheros simultáneamente, pero sí puedes ejecutar el programa varias veces.
Si queréis saber qué es capaz de hacer este programa, podéis consultar las entradas de este blog sobre HHJReader: http://isabella70.blogspot.com/search?q=hhjreader
Para descargarlo podéis usar el siguiente enlace (no he encontrado ningún hosting mejor): http://www.filefactory.com/file/a2ga953/n/HHJReader_v2-0_zip
El programa se suministra "tal cual", no garantizamos ningún tipo de soporte ni ayuda.
Sigo jugando
Después de las vacaciones he vuelto a jugar pero, (a) estoy jugando bastante menos y (b) no estoy "investigando". Por eso no publico nada, porque no tengo nada que contar.
Voy a intentar elaborar algo sobre estrategia HU orientado a S&G y MTT, el título sería "Estrategias para HU con stacks muy diferentes"
¿"pocker"?
Los de la cadena SER han inventado hoy la palabra "pocker". ¿de dónde lo han sacado? ¿no tiene google?


Poker básico. Calcular odds usando la "regla del 4"
Anónimo (gran lector de blogs) preguntaba en una entrada anterior (Vamos a contar OUTs) dos cosas:
Q: "No sé si este blog sigue abierto"
A: Este blog sigue abierto. Habrá nuevos contenidos cuando elaboremos más material.
Q: "en el metodo abreviado ese para el calculo [de odds], me podrias decir de donde viene el 8 ese"
A: Se trata de la famosa "regla del 4"
Calcular ODDs en el TURN usando la regal del 4
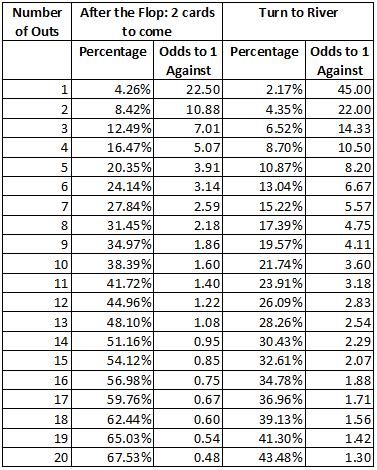
Todos conocemos las tablas de ODDs como la que adjunto al final de esta entrada. Pues bien para calcular mentalmente los odds en el turn solo hay que aplicar la "famosa" regla del cuatro.
Si el número de OUTs es menor de 8:
Si el número de OUTs es mayor de 8:
Se puede comprobar en la tabla que la fórmula [1] funciona cuando el número de OUTs es menor de 8. Cuando es mayor se puede aplicar la fórmula [2] como hicimos en la entrada de la polémica: Vamos a contar OUTs
Background matemático
¿por qué funciona la regla del 4? La probabilidad de 1 OUT en el TURN es 4,25%
4,25% = 1 - (46/47) * (45/46)
Entonces la probabilidad de varios OUTs se puede aproximar multiplicando el número de OUTs por 4% que es, aproximadamente, la probabilidad de un OUT. La corrección cuando el número de OUTs es mayor de 8 es necesaria porque cuando aumenta el número de OUTs aumenta la probabilidad de que coincida uno de los OUTs en el TURN y otro en el RIVER.
La regla del 2
La regla del 2 es muy simple. Para calcular los ODDs en el RIVER sólo hay que multiplicar el número de OUTs por 2. Si se quiere mayor precisión se debería multiplicar por 2,17% que es la probabilidad de que salga un OUT en el RIVER:
2,17% = 1/46
La regla del 2 no necesita ninguna corrección como se puede comprobar en la tabla.
Q: "No sé si este blog sigue abierto"
A: Este blog sigue abierto. Habrá nuevos contenidos cuando elaboremos más material.
Q: "en el metodo abreviado ese para el calculo [de odds], me podrias decir de donde viene el 8 ese"
A: Se trata de la famosa "regla del 4"
Calcular ODDs en el TURN usando la regal del 4
Todos conocemos las tablas de ODDs como la que adjunto al final de esta entrada. Pues bien para calcular mentalmente los odds en el turn solo hay que aplicar la "famosa" regla del cuatro.
Si el número de OUTs es menor de 8:
ODDs (%) = OUTs * 4 [1]
Si el número de OUTs es mayor de 8:
ODDs (%) = OUTs * 4 - (OUTs - 8) [2]
Se puede comprobar en la tabla que la fórmula [1] funciona cuando el número de OUTs es menor de 8. Cuando es mayor se puede aplicar la fórmula [2] como hicimos en la entrada de la polémica: Vamos a contar OUTs

Background matemático
¿por qué funciona la regla del 4? La probabilidad de 1 OUT en el TURN es 4,25%
4,25% = 1 - (46/47) * (45/46)
Entonces la probabilidad de varios OUTs se puede aproximar multiplicando el número de OUTs por 4% que es, aproximadamente, la probabilidad de un OUT. La corrección cuando el número de OUTs es mayor de 8 es necesaria porque cuando aumenta el número de OUTs aumenta la probabilidad de que coincida uno de los OUTs en el TURN y otro en el RIVER.
La regla del 2
La regla del 2 es muy simple. Para calcular los ODDs en el RIVER sólo hay que multiplicar el número de OUTs por 2. Si se quiere mayor precisión se debería multiplicar por 2,17% que es la probabilidad de que salga un OUT en el RIVER:
2,17% = 1/46
La regla del 2 no necesita ninguna corrección como se puede comprobar en la tabla.
Arthur Benjamin. "Matemago"
Arthur Benjamin habla sobre el posicionamiento del Cálculo (antiguo, aburrido, continuo) frente a la Estadísticas (moderno, divertido, discreto). Bueno, es una opinión.
Poker básico con ejemplos. Vamos a contar OUTs
Contar OUTs es básico, muy básico. Observe, el lector, la siguiente mano:
No Limit Holdem Tournament
$5.00+$0.20
10 players
Converted at weaktight.com
Blinds: 15/30
Pre-flop: (45, 10 players) Hero is BB


1 fold, Dominus666 (UTG+2) raises to 360, 7 folds, Hero calls 330
> Las ciegas están en 15/30. Estamos en la ciega grande, y Dominus desde UTG+2 sube 360 (normal, tiene QQ). Con KQs vamos a defender nuestra ciega.
Main Pot (735)
Flop:
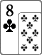
 (735, 2 players)
(735, 2 players)
Hero checks, Dominus666 goes all-in 1,060,
Flop interesante, Dominus mete la caja. Estamos en las primeras manos del S&G, no tenemos nada ("K high") pero tenemos algunos OUTs.
¿cuántos OUTs tenemos?
1. vamos a suponer que el rival tiene AA, AKs, AKo o KK. En el "peor" de los casos podría tener JJ y haber pillado set máximo en el flop.
2. en todos los casos anteriores las siguientes cartas nos dan jugada ganadora:
- todos los corazones: 9
- todos los ases (excepto el de corazones que ya está contado): 3
- todos los nueves: 3
3. A esto sumamos los reyes que nos darían una pareja superior que la del rival: 3
4. En total, tenemos 18 outs, quedan 47 cartas ocultas y aún tienen que salir 2 cartas. Esto es, aproximadamente, un 62%.
Método abreviado: 18 (outs) * 4 (turn+river) - 10 (18 - 8) = 62%
Es decir, hay más del 50% de posiblidad de completar la jugada. INSTA-CALL
Hero calls 1,060
Main Pot (2,855)
Turn: (2,855, 2 players)
(2,855, 2 players)
El TURN falló
Main Pot (2,855)
River: (2,855, 3 players)
(2,855, 3 players)
El RIVER "acertó"
Main Pot (2,855)
Final Pot: 2,855
Hero shows:

Dominus666 shows:
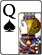
Escalera real de color, jugada máxima y bote ganado
En este caso no hay que calcular los odds del bote porque nuestra probabilidad de ganar (equity) es mayor de 0,5. Como tenemos más probabilidad de ganar que de perder cualquier bote nos va a dar un EV positivo.
No Limit Holdem Tournament
$5.00+$0.20
10 players
Converted at weaktight.com
Blinds: 15/30
Pre-flop: (45, 10 players) Hero is BB


1 fold, Dominus666 (UTG+2) raises to 360, 7 folds, Hero calls 330
> Las ciegas están en 15/30. Estamos en la ciega grande, y Dominus desde UTG+2 sube 360 (normal, tiene QQ). Con KQs vamos a defender nuestra ciega.
Main Pot (735)
Flop:

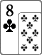
 (735, 2 players)
(735, 2 players)Hero checks, Dominus666 goes all-in 1,060,
Flop interesante, Dominus mete la caja. Estamos en las primeras manos del S&G, no tenemos nada ("K high") pero tenemos algunos OUTs.
¿cuántos OUTs tenemos?
1. vamos a suponer que el rival tiene AA, AKs, AKo o KK. En el "peor" de los casos podría tener JJ y haber pillado set máximo en el flop.
2. en todos los casos anteriores las siguientes cartas nos dan jugada ganadora:
- todos los corazones: 9
- todos los ases (excepto el de corazones que ya está contado): 3
- todos los nueves: 3
3. A esto sumamos los reyes que nos darían una pareja superior que la del rival: 3
4. En total, tenemos 18 outs, quedan 47 cartas ocultas y aún tienen que salir 2 cartas. Esto es, aproximadamente, un 62%.
Método abreviado: 18 (outs) * 4 (turn+river) - 10 (18 - 8) = 62%
Es decir, hay más del 50% de posiblidad de completar la jugada. INSTA-CALL
Hero calls 1,060
Main Pot (2,855)
Turn:
 (2,855, 2 players)
(2,855, 2 players)El TURN falló
Main Pot (2,855)
River:
 (2,855, 3 players)
(2,855, 3 players)El RIVER "acertó"
Main Pot (2,855)
Final Pot: 2,855
Hero shows:


Dominus666 shows:

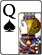
Escalera real de color, jugada máxima y bote ganado
En este caso no hay que calcular los odds del bote porque nuestra probabilidad de ganar (equity) es mayor de 0,5. Como tenemos más probabilidad de ganar que de perder cualquier bote nos va a dar un EV positivo.
Crack of doom
Ultimamente, mis entradas están poco elaboradas. Es el calor y las ganas de vacaciones.
Os dejo un "corto" de Hitchcock ("Hitch" & "Cock", ¿nadie se había dado cuenta antes?) que trata sobre poker y los faroles, siempre tan cinematográficos.
Os dejo un "corto" de Hitchcock ("Hitch" & "Cock", ¿nadie se había dado cuenta antes?) que trata sobre poker y los faroles, siempre tan cinematográficos.
Doble o Nada. Tengo ganas de volver a jugar a Poker
Llevo unas semanas jugando, exclusivamente, DoN (Doble o Nada) en modalidad turbo (las ciegas suben cada 5 minutos). El motivo principal (y único) es que tengo un bono de PokerStars que caduca en septiembre; lo quiero completar antes de irme de vacaciones y ésta me parece la manera más rápida y segura.
Así que ya puedo confirmar lo que se oye por los foros: DoN es una modalidad "fácil" donde uno puede mantenerse en beneficios si sigue las reglas al pie de la letra.
En esta entrada de Poker Red hay una guía bastante completa de cómo afrontar un DoN: Guia de DON por Tomas "StarteCh" Recart.
En resumen, no hay que empeñarse en ganar todas las fichas, si las cosas van bien no hay que arriesgar en flips tontos (aunque tengas KK) y no hay que empeñarse en eliminar a los short-stacks, ya lo hacen ellos solos.
El problema de los DoN es que se repiten mucho los mismos movimientos: robo de ciegas, value bets con nuts, set mining y, en la última fase, all-in si vamos muy cortos o sitout si tenemos margen suficiente. Así que estoy deseando conseguir el puto bono, irme de vacaciones y, cuando vuelva, jugar poker de verdad (MTT).
Así que ya puedo confirmar lo que se oye por los foros: DoN es una modalidad "fácil" donde uno puede mantenerse en beneficios si sigue las reglas al pie de la letra.
En esta entrada de Poker Red hay una guía bastante completa de cómo afrontar un DoN: Guia de DON por Tomas "StarteCh" Recart.
En resumen, no hay que empeñarse en ganar todas las fichas, si las cosas van bien no hay que arriesgar en flips tontos (aunque tengas KK) y no hay que empeñarse en eliminar a los short-stacks, ya lo hacen ellos solos.
El problema de los DoN es que se repiten mucho los mismos movimientos: robo de ciegas, value bets con nuts, set mining y, en la última fase, all-in si vamos muy cortos o sitout si tenemos margen suficiente. Así que estoy deseando conseguir el puto bono, irme de vacaciones y, cuando vuelva, jugar poker de verdad (MTT).
Leo queda, definitivamente, en el puesto 27 del ME de WSOP
Puesto 27 del Main Event de las World Series of Poker. Muchísimas felicidades desde aquí!
Nunca pensé que dedicaría un post de este tipo a un jugador (y este es el segundo). Al fin y al cabo, esta chica nos ha tenido dos noches sin dormir enganchados al foro de Poker Red
La mano de la eliminación que no tiene mayor historia, aunque seguro que a Leo nunca se le olvidará (Fuente: WSOP):
There will not be a woman at the final table of the Main Event this year. After Warren Zackey opened the pot to 350,000 preflop, Leo Margets put all of her chips at risk and shoved all in.
Zackey called with Ah Th and found himself in a dominating position against Margets' As 7h. Margets was left looking for running cards after a flop of 4c 8d Ts. She didn't get them. The turn and river fell 4h and 2c to make her the first eliminated player of the day.
Nunca pensé que dedicaría un post de este tipo a un jugador (y este es el segundo). Al fin y al cabo, esta chica nos ha tenido dos noches sin dormir enganchados al foro de Poker Red
La mano de la eliminación que no tiene mayor historia, aunque seguro que a Leo nunca se le olvidará (Fuente: WSOP):
There will not be a woman at the final table of the Main Event this year. After Warren Zackey opened the pot to 350,000 preflop, Leo Margets put all of her chips at risk and shoved all in.
Zackey called with Ah Th and found himself in a dominating position against Margets' As 7h. Margets was left looking for running cards after a flop of 4c 8d Ts. She didn't get them. The turn and river fell 4h and 2c to make her the first eliminated player of the day.
Go Leo (Margets)!
Leo Margets ha llegado al octavo día del Main Event de Holdem de las World Series de poker (WSOP). Empezaron 6.500 jugadores de todo el mundo, y ya solo quedan 27. Los 648 primeros cobran premio (21.000$ el 648 y 8,500.000$ el primero). Leo ya tiene garantizados los 350.000$ del puesto 27 pero, aunque está muy corta de fichas, sigue soñando con estar en la mesa final en otoño (los 9 primeros "quedan" para jugar la mesa final el 7 de noviembre).
Moltes felicitats, nena!!!
ps. el mejor seguimiento en el foro de poker-red gracias, especialmente, al seguimiento en vivo realizado por Pacocho
Moltes felicitats, nena!!!
ps. el mejor seguimiento en el foro de poker-red gracias, especialmente, al seguimiento en vivo realizado por Pacocho
Matemáticas no tan básicas. Teorema de Bayes
El teorema de Bayes relaciona la probabilidad de ocurrencia de un suceso a partir de la constatación de un hecho (un "hecho cierto") cuya probabilidad de que ocurra está condicionado al primero. No se entiende muy bien, ¿verdad?
Otra forma de verlo: el suceso A depende de B, ¿cómo puedo precisar la probabilidad de A si ya sabemos que B ha ocurrido y conocemos en qué grado B depende A? Ojo, "B depende de A" (su grado de dependencia) es lo opuesto de lo que queremos calcular.
En la práctica y explicado de moda intuitiva: Bayes sirve para corregir una estimación (una probabilidad) con la información que vamos recopilando. En el caso del Poker, tenemos una estimación inicial que según avanza la mano podemos corregir con la información que vamos recibiendo.
ENUNCIADO Y DEMOSTRACIÓN MATEMATICA

(1) es la probabilidad de que los sucesos A y B ocurran. Su valor es la probabilidad de que ocurra A -P(A)- multiplicado por la probabilidad de "que ocurra B si A ha ocurrido -P(B|A)-". Esta igualdad es intuitiva y conmutativa.
(2.1) aplicamos (1) para despejar P(A|B).
(2.2) En el numerador volvemos a aplicar (1) y en el denominador sustituimos P(B) ("probabilidad de que ocurra B") por "la probabilidad de que ocurra B si ocurre A (según la probabilidad de A) y la probabilidad de B si no ocurre A (según la probabilidad de que no ocurra A)".
Esto último siempre es cierto (porque A siempre "o se cumple o no se cumple")
(3) Es la fórmula genérica de Bayes.
EJEMPLO PRÁCTICO
Ahora vamos a poner un ejemplo aplicado al poker. Imagina que recibes KQo y estás jugando HU contra el mejor jugador del mundo que, además, ha adivinado (o visto) tu jugada.
Tu rival, además de ser clarividente, se juega un 15% de faroles, es decir, hay un 15% de probabilidades de que no teniendo una jugada mejor que la de su rival haga una subida.
Por otra parte, tu rival hace slowplay el 10% de las veces, es decir, hay un 10% de probabilidades de que teniendo una jugada mejor que la de su rival no suba. O lo que es lo mismo, el 90% de las veces que tiene una buena jugada hace una apuesta por valor (value bet).
Fijaros que 15% (porcentaje de faroles) y 90% (porcentaje de value bets) no suman 100% ¿por qué? porque son dos sucesos independientes: nuestro rival puede aumentar su ratio de faroles sin cambiar el ratio de slowplay.
Vamos a suponer que hay un 11,8% de manos mejores que KQo (88,2% de las posibles manos serían peores).
Pues bien, tu rival sube y quieres saber cuál es la probabilidad de que tenga una jugada mejor que la tuya.
Datos de partida para poder aplicar Bayes:
- P(Raise|Jugada) = 90%. Probabilidad de que el villano haga raise si tiene jugada
- P(Raise|No_Jugada) = 15%. Idem si no tiene jugada (farol = bluff)
- P(Jugada) = 88,2%. Probabilidad de que tenga una jugada (mejor que la nuestra)
- P(No_Jugada) = 11,8%. Probabilidad de que no tenga jugada
- P(Jugada) + P(No_Jugada) = 1. La probabilidad de tener o no tener jugada son complementarias y suman 1.
¿qué queremos calcular?
Queremos conocer P(Jugada|Raise) que es "la probabilidad de que este cabrón tenga una jugada mejor que nosotros ahora que hemos visto que ha subido".
P(Jugada|Raise) = P(Raise|Jugada) * P(Jugada) / ( P(R|J)*P(J) + P(R|N)*P(N) ) = 0,44
Con estas condiciones el villano tiene una probabilidad de tener una jugada mejor que la nuestra de un 44%
Curioso, ¿no?
Como el villano hace value bet casi siempre (90%) y sólo hace faroles unas pocas veces (15%) parecería que casi siempre que apuesta debería tener una jugada y, sin embargo, el 56% de las veces que apuesta no tiene nada.
Referencias: El teorema de Bayes en Wikipedia
Otra forma de verlo: el suceso A depende de B, ¿cómo puedo precisar la probabilidad de A si ya sabemos que B ha ocurrido y conocemos en qué grado B depende A? Ojo, "B depende de A" (su grado de dependencia) es lo opuesto de lo que queremos calcular.
En la práctica y explicado de moda intuitiva: Bayes sirve para corregir una estimación (una probabilidad) con la información que vamos recopilando. En el caso del Poker, tenemos una estimación inicial que según avanza la mano podemos corregir con la información que vamos recibiendo.
ENUNCIADO Y DEMOSTRACIÓN MATEMATICA

(1) es la probabilidad de que los sucesos A y B ocurran. Su valor es la probabilidad de que ocurra A -P(A)- multiplicado por la probabilidad de "que ocurra B si A ha ocurrido -P(B|A)-". Esta igualdad es intuitiva y conmutativa.
(2.1) aplicamos (1) para despejar P(A|B).
(2.2) En el numerador volvemos a aplicar (1) y en el denominador sustituimos P(B) ("probabilidad de que ocurra B") por "la probabilidad de que ocurra B si ocurre A (según la probabilidad de A) y la probabilidad de B si no ocurre A (según la probabilidad de que no ocurra A)".
Esto último siempre es cierto (porque A siempre "o se cumple o no se cumple")
(3) Es la fórmula genérica de Bayes.
EJEMPLO PRÁCTICO
Ahora vamos a poner un ejemplo aplicado al poker. Imagina que recibes KQo y estás jugando HU contra el mejor jugador del mundo que, además, ha adivinado (o visto) tu jugada.
Tu rival, además de ser clarividente, se juega un 15% de faroles, es decir, hay un 15% de probabilidades de que no teniendo una jugada mejor que la de su rival haga una subida.
Por otra parte, tu rival hace slowplay el 10% de las veces, es decir, hay un 10% de probabilidades de que teniendo una jugada mejor que la de su rival no suba. O lo que es lo mismo, el 90% de las veces que tiene una buena jugada hace una apuesta por valor (value bet).
Fijaros que 15% (porcentaje de faroles) y 90% (porcentaje de value bets) no suman 100% ¿por qué? porque son dos sucesos independientes: nuestro rival puede aumentar su ratio de faroles sin cambiar el ratio de slowplay.
Vamos a suponer que hay un 11,8% de manos mejores que KQo (88,2% de las posibles manos serían peores).
Pues bien, tu rival sube y quieres saber cuál es la probabilidad de que tenga una jugada mejor que la tuya.
Datos de partida para poder aplicar Bayes:
- P(Raise|Jugada) = 90%. Probabilidad de que el villano haga raise si tiene jugada
- P(Raise|No_Jugada) = 15%. Idem si no tiene jugada (farol = bluff)
- P(Jugada) = 88,2%. Probabilidad de que tenga una jugada (mejor que la nuestra)
- P(No_Jugada) = 11,8%. Probabilidad de que no tenga jugada
- P(Jugada) + P(No_Jugada) = 1. La probabilidad de tener o no tener jugada son complementarias y suman 1.
¿qué queremos calcular?
Queremos conocer P(Jugada|Raise) que es "la probabilidad de que este cabrón tenga una jugada mejor que nosotros ahora que hemos visto que ha subido".
P(Jugada|Raise) = P(Raise|Jugada) * P(Jugada) / ( P(R|J)*P(J) + P(R|N)*P(N) ) = 0,44
Con estas condiciones el villano tiene una probabilidad de tener una jugada mejor que la nuestra de un 44%
Curioso, ¿no?
Como el villano hace value bet casi siempre (90%) y sólo hace faroles unas pocas veces (15%) parecería que casi siempre que apuesta debería tener una jugada y, sin embargo, el 56% de las veces que apuesta no tiene nada.
Referencias: El teorema de Bayes en Wikipedia
Elige: AKo, JTs o 22 ?
- ¿qué mano prefieres: AKo, JTs o 22?
- elige tú primero y luego te digo...
Es sólo un juego pero, comparando las probabilidades de éxito de cada jugada en las diferentes combinaciones posibles, llegamos a una conclusión ya conocida pero que conviene recordar de vez en cuando: la fuerza de nuestra jugada depende de las jugadas que tegan nuestros rivales
La tabla resume las probabilidades de victoria de cada mano dependiendo de la mano con la que se enfrente. AKo pierde frente a 22 y gana frente a JTs que, a su vez, gana a 22.

El caso paradigmático es la pareja menor (22 casi nunca es favorito) cuando se enfrenta a AK, una de las mejores manos iniciales. El jugador con AK hace shove y, cuando pierde frente al "pringao" de la pareja, se queja de su mala suerte.
- elige tú primero y luego te digo...
Es sólo un juego pero, comparando las probabilidades de éxito de cada jugada en las diferentes combinaciones posibles, llegamos a una conclusión ya conocida pero que conviene recordar de vez en cuando: la fuerza de nuestra jugada depende de las jugadas que tegan nuestros rivales
La tabla resume las probabilidades de victoria de cada mano dependiendo de la mano con la que se enfrente. AKo pierde frente a 22 y gana frente a JTs que, a su vez, gana a 22.

El caso paradigmático es la pareja menor (22 casi nunca es favorito) cuando se enfrenta a AK, una de las mejores manos iniciales. El jugador con AK hace shove y, cuando pierde frente al "pringao" de la pareja, se queja de su mala suerte.
A6o de mano. Mi peor pesadilla
Esto no tiene ninguna base científica pero creo que nos pasa a muchos jugadores. Hay jugadas de mano que de forma irracional resultan "irresistibles". En mi caso, cuando recibo A6o siempre intento jugarla, es la jugada que más fichas me cuesta con diferencia.


En los últimos tres días he recibido esta jugada 20 veces, la he jugado 18 veces (1 vez desde BB) y he perdido fichas todas las veces.


En los últimos tres días he recibido esta jugada 20 veces, la he jugado 18 veces (1 vez desde BB) y he perdido fichas todas las veces.
DoN super pasivo
Hay gente que comenta que los S&G DoN es el refugio de los jugadores más pasivos. Personalmente me gustan más los S&G "normales" donde puedes, si todo va bien, practicar en una misma partida situaciones de todo tipo: Full ring, Short Handed, Heads Up, Deep Stack, Antes, etc.
Anoche jugué una de las mesas más pasivas que recuerdo: el PFR medio por debajo del 10% y, si os fijáis en la imagen de las manos jugadas, comprobaréis que se vieron muy pocos flops.... 30 manos se resolvieron sin ver el flop (de un total de 57 manos).

He cargado la sesión en Weaktight:

Fuente: weaktight.com
Anoche jugué una de las mesas más pasivas que recuerdo: el PFR medio por debajo del 10% y, si os fijáis en la imagen de las manos jugadas, comprobaréis que se vieron muy pocos flops.... 30 manos se resolvieron sin ver el flop (de un total de 57 manos).

He cargado la sesión en Weaktight:

Fuente: weaktight.com
Programación . Cálculo del ICM
ICM significa Independent Chip Model y, de forma muy resumida, es un modelo que sirve para calcular el valor de las fichas (chips) durante la disputa de un torneo (S&G o MTT). La idea detrás de ICM es que las decisiones en un torneo no se pueden basar, como en Cash, en el valor nominal de las fichas.
Intuitivamente esto ya lo sabíamos: en una mesa de Cash hay 300$ en el bote, la cantidad a subir o los pot odds para ver una apuesta de 10$ se pueden calcular directamente. Sin embargo, en un S&G, si sólo te quedan 10$ sólo los deberías jugar con un equity mayor de 0,5; otro ejemplo, si tienes 6.000$ y uno de los rivales tiene 290$ puedes hacerle shove con un rango bastante amplio porque 290$ de tu pila valen mucho menos que los últimos 290$ de su pila; un tercer ejemplo, sigues con 6.000$, tienes TT y un rival con más fichas hace shove, en este caso la intuición (del cash) te dice que es una buena oportunidad para ganar 6.000$ mientras que ICM te recuerda que perder 6.000$ significa perder el torneo y que deberías hacer fold. En ICM, 12.000$ nunca es el doble de 6.000$, es bastante menos
En el foro de Poker red Sergeon colgó una introducción a ICM a partir de varios artículos, a su vez, del foro 2+2.
Vamos a incorporar algunos cálculos basados en ICM a HHJReader (estupendo programa). De momento, hemos programado una calculadora de ICM en Excel. Aquí vemos el resultado y el código utilizado (traducido a VBA a partir de JAVA). Con este código cualquiera puede construirse su propia calculadora usando Excel o, directamente, en Visual Basic.

El código:
Existen en Internet muchas calculadoras de ICM, por ejemplo en, como no, ICM Poker.
El código en Java lo hemos sacado de POKERAI. ICM Equity Calculator (Pokerai).
Intuitivamente esto ya lo sabíamos: en una mesa de Cash hay 300$ en el bote, la cantidad a subir o los pot odds para ver una apuesta de 10$ se pueden calcular directamente. Sin embargo, en un S&G, si sólo te quedan 10$ sólo los deberías jugar con un equity mayor de 0,5; otro ejemplo, si tienes 6.000$ y uno de los rivales tiene 290$ puedes hacerle shove con un rango bastante amplio porque 290$ de tu pila valen mucho menos que los últimos 290$ de su pila; un tercer ejemplo, sigues con 6.000$, tienes TT y un rival con más fichas hace shove, en este caso la intuición (del cash) te dice que es una buena oportunidad para ganar 6.000$ mientras que ICM te recuerda que perder 6.000$ significa perder el torneo y que deberías hacer fold. En ICM, 12.000$ nunca es el doble de 6.000$, es bastante menos
En el foro de Poker red Sergeon colgó una introducción a ICM a partir de varios artículos, a su vez, del foro 2+2.
Vamos a incorporar algunos cálculos basados en ICM a HHJReader (estupendo programa). De momento, hemos programado una calculadora de ICM en Excel. Aquí vemos el resultado y el código utilizado (traducido a VBA a partir de JAVA). Con este código cualquiera puede construirse su propia calculadora usando Excel o, directamente, en Visual Basic.

El código:
' Calculo de ICM en VBA para excel
' Autor (de la adaptación a VBA): Isabella70
' Fecha: 2009-06-10
' Fuente de las fórmulas en JAVA: http://pokerai.org/wiki/index.php/ICM_Equity_Calculator
'
' Uso:
' - la función recibe un número (1-n) que es id del jugador
' - "Payoffs" es un rango en el excel (una columna) que tiene los premios a repartir
' (pueden ser porcentajes o neto)
' - "Pilas" es otro rango del excel (otra columna) que contiene las pilas actuales
' de los jugadores
Function getEquity(i)
' la función recibe el jugador cuyo EV queremos calcular
currentPlayer = i
premios = Range("Payoffs")
pilas = Range("Pilas")
' calculamos el total de chips
Dim total As Double
total = 0
For Each chip In pilas
' hay tantos jugadores como pilas diferente de 0
If chip = 0 Then
Exit For
End If
total = total + chip
Next chip
' la función recursiva calcula el EV del jugador en cada nivel
' 1 si es el ganador, 2 si es el segundo, etc.
getEquity = getEquityRecursivo(premios, pilas, total, currentPlayer, 1)
End Function
Function getEquityRecursivo(payouts, stacks, total, player, depth)
Dim eq As Double
' los rangos son bidimensionales, en este caso siempre hay 1 columna
stack_player = stacks(player, 1)
payout_puesto = payouts(depth, 1)
' EV: probabilidad de ganar por premio
' la probabilidad es la relación entre las fichas del jugador y todas las fichas en juego
eq = payout_puesto * stack_player / total
' sólo calculamos el EV de los puestos con premio, el resto es 0
If depth <= UBound(payouts) Then
For ist = 1 To UBound(stacks)
st = stacks(ist, 1)
If ist <> player And st > 0 Then
Dim c As Double
c = stacks(ist, 1)
stacks(ist, 1) = 0
' Debug.Print "+ Player: " & player & " depth: " & depth & " eq: " & eq
eq = eq + getEquityRecursivo(payouts, stacks, total - st, player, depth + 1) * st / total
' Debug.Print "- Player: " & player & " depth: " & depth & " eq: " & eq
stacks(ist, 1) = c
End If
Next ist
End If
getEquityRecursivo = eq
End Function
Existen en Internet muchas calculadoras de ICM, por ejemplo en, como no, ICM Poker.
El código en Java lo hemos sacado de POKERAI. ICM Equity Calculator (Pokerai).
Matemáticas no tan básicas. Riesgo de ruina
En la entrada anterior sobre la varianza demostramos mediante la simulación del resultado de torneos S&G que, conocida la distribución de los resultados, se puede calcular con bastante precisión la varianza de estos resultados. Podemos calcular la varianza pero eso no evita que las ganancias evolucionen de forma, aparentemente, caprichosa e imprevisible.
En esta entrada vamos a analizar el Riesgo de ruina (Risk of Ruin)
¿qué es el riesgo de ruina? es la probabilidad de que nuestro saldo llegue a 0 (bancarrota), considerando que partimos de un saldo inicial, que reinvertimos todas las ganancias, que las características del juego se mantienen constantes y que jugamos indefinidamente.
Las fórmulas están sacadas del excelente libro Mathematics of Poker, donde se demuestran los desarrollos y se profundiza bastante en otros aspectos (por ejemplo, cómo calcular el riesgo de ruina sin tener un winrate constante).
Las fórmulas que permiten calcular el Riesgo de ruina (RoR) son las siguientes:

En (1), vemos que el RoR depende de un factor constante (alfa) y de nuestro saldo inicial (B). El factor alfa está relacionado, de alguna manera, con el EV de nuestro juego. De manera que si el EV es negativo, el RoR es 1 (100%, seguro, indudable, incuestionable). Primera conclusión: lo primero que hay que hacer es ser ganador porque, si no, acabaremos arruinados "sí-o-sí".
La fórmula (2) permite calcular el RoR sin calcular previamente el factor alfa utilizando, en su lugar, la media y la desviación típica cuadrada (la varianza). Para usar esta fórmula necesitamos que los resultados de nuestro juego se ajustan a una distribución normal. Esta fórmula no se puede usar para calcular el RoR de tórneos cuyos resultados no se ajustan a una distribución normal. Ojo: los resultados de un jugador ganador en torneos no siguen una distribución normal, ya que son, necesariamente, asimétricos (y con curtosis).
Esta fórmula la pueden usar los jugadores de mesas NL que sí tienen una distribución normal de sus ganancias.
Simulaciones
He reproducido, lo más fielmente posible, el escenario de mi juego actual y he simulado 10.000 partidas (torneos) con los resultados que podéis ver al final.
Escenario
- Torneos S&G de 9 jugadores, 50,5$ de entrada y premios para los tres primeros (22,5$, 13,5$ y 9$).
- Resultados en forma de probabilidad de quedar en los tres primeros puestos: 0,10, 0,15 y 0,15. El resto de puestos (sin premio) se reparten el 0,6 restante. Estos son mis resultados en los últimos 100 torneos (aproximadamente).
- Entramos en premios en el 40% de los torneos.
- EV por torneo: 0,69$ (0,125). Positivo como debe ser.
Resultado
Calcular alfa requiere resolver la ecuación (1) para varios valores de B. Con excel se puede resolver la ecuación por métodos numéricos ("iSolver" lo llama Microsoft, "Análisis Y si" en español).
Para el escenario descrito alfa vale 0,00063397
Una vez calculado alfa podemos aplicar (1) para diferentes valores de B ("banca" o "saldo" inicial) y obtener una tabla como la que sigue:
Recordemos que el RoR se cálcula sobre "infinitas" ejecuciones y no tiene en cuenta cambios de nivel, reintegros o nuevas aportaciones a nuestra cuenta que no sean los propios torneos ganados o perdidos.
A continuación se muestra el resultado de ejecutar la simulación con diferentes saldos iniciales.



En esta entrada vamos a analizar el Riesgo de ruina (Risk of Ruin)
¿qué es el riesgo de ruina? es la probabilidad de que nuestro saldo llegue a 0 (bancarrota), considerando que partimos de un saldo inicial, que reinvertimos todas las ganancias, que las características del juego se mantienen constantes y que jugamos indefinidamente.
Las fórmulas están sacadas del excelente libro Mathematics of Poker, donde se demuestran los desarrollos y se profundiza bastante en otros aspectos (por ejemplo, cómo calcular el riesgo de ruina sin tener un winrate constante).
Las fórmulas que permiten calcular el Riesgo de ruina (RoR) son las siguientes:

En (1), vemos que el RoR depende de un factor constante (alfa) y de nuestro saldo inicial (B). El factor alfa está relacionado, de alguna manera, con el EV de nuestro juego. De manera que si el EV es negativo, el RoR es 1 (100%, seguro, indudable, incuestionable). Primera conclusión: lo primero que hay que hacer es ser ganador porque, si no, acabaremos arruinados "sí-o-sí".
La fórmula (2) permite calcular el RoR sin calcular previamente el factor alfa utilizando, en su lugar, la media y la desviación típica cuadrada (la varianza). Para usar esta fórmula necesitamos que los resultados de nuestro juego se ajustan a una distribución normal. Esta fórmula no se puede usar para calcular el RoR de tórneos cuyos resultados no se ajustan a una distribución normal. Ojo: los resultados de un jugador ganador en torneos no siguen una distribución normal, ya que son, necesariamente, asimétricos (y con curtosis).
Esta fórmula la pueden usar los jugadores de mesas NL que sí tienen una distribución normal de sus ganancias.
Simulaciones
He reproducido, lo más fielmente posible, el escenario de mi juego actual y he simulado 10.000 partidas (torneos) con los resultados que podéis ver al final.
Escenario
- Torneos S&G de 9 jugadores, 50,5$ de entrada y premios para los tres primeros (22,5$, 13,5$ y 9$).
- Resultados en forma de probabilidad de quedar en los tres primeros puestos: 0,10, 0,15 y 0,15. El resto de puestos (sin premio) se reparten el 0,6 restante. Estos son mis resultados en los últimos 100 torneos (aproximadamente).
- Entramos en premios en el 40% de los torneos.
- EV por torneo: 0,69$ (0,125). Positivo como debe ser.
Resultado
Calcular alfa requiere resolver la ecuación (1) para varios valores de B. Con excel se puede resolver la ecuación por métodos numéricos ("iSolver" lo llama Microsoft, "Análisis Y si" en español).
Para el escenario descrito alfa vale 0,00063397
Una vez calculado alfa podemos aplicar (1) para diferentes valores de B ("banca" o "saldo" inicial) y obtener una tabla como la que sigue:
Saldo RoRSegunda conclusión: el RoR decrece exponencialmente. Para jugar tranquilos S&G de 5,5$ de entrada necesitaríamos 500$ (90 veces la entrada).
20 98,74%
50 96,87%
100 93,85%
250 85,34%
500 72,83%
1000 53,04%
Recordemos que el RoR se cálcula sobre "infinitas" ejecuciones y no tiene en cuenta cambios de nivel, reintegros o nuevas aportaciones a nuestra cuenta que no sean los propios torneos ganados o perdidos.
A continuación se muestra el resultado de ejecutar la simulación con diferentes saldos iniciales.



Matemáticas no tan básicas. La varianza
(me ha quedado una entrada un poco densa e ininteligible. lo siento. ininteligible es inteligible? lo dudo)
La puta varianza!
La varianza es el nombre técnico que dan los jugadores de poker a una racha de mala suerte. La varianza justifica que aunque un jugador esté jugando bien esté, a su vez, perdiendo: todas sus acciones tienen EV positivo pero su banca registra pérdidas. Los jugadores dicen (decimos) que no importa perder porque "ha sido culpa de la varianza". El buen jugador de poker parece que sólo tiene un enemigo: la varianza.
Para defenderse de la varianza lo más común es mejorar la gestión de los recursos propios (banca) para que "un zarpazo de la varianza" no termine en "bancarrota". Es decir que una racha negativa no acabe con toda nuestra banca y podamos seguir jugando hasta que llegue una racha positiva.
Mi opinión:
la varianza existe (sin duda) pero no es la única culpable de nuestras perdidas. Además de la varianza, existen otros "culpables" como, por ejemplo, nuestros rivales que son cada vez más y mejores. Y más peligroso que la varianza estadística (aleatoria) es la inestabilidad del nivel de juego propio. Contra la varianza: jugar cada vez mejor y, a ser posible, mejor que los rivales.
Bueno, después del inciso, vamos a explicar qué es la varianza y cómo se calcula. Luego presentaremos unas simulaciones donde intentamos demostrar que la varianza, paradójicamente, siempre tienda a cumplirse.
Definición de varianza
La varianza es el cuadrado de la desviación típica, es decir hay una relación directa entre ambas. Yo siempre usé "desviación típica" pero es más sonoro "varianza" y es el término que se usa normalmente en los foros, artículos y libros de poker.
La varianza mide la dispersión de una muestra en función de la diferencia (la distancia) de cada uno de los elementos de la muestra con el valor medio de la misma.
En un caso extremo, si la varianza es nula (0) todos los elementos de la muestra tienen el mismo valor que coincide con el valor medio de la misma. Si tengo 10 sacos que pesan 25 kg cada uno {25, 25, 25, 25, 25, 25, 25, 25, 25, 25}: el peso medio es 25 y la varianza de la muestra es 0.
Otros ejemplos
Ejemplo 1: en una clase hay 10 niños cuyas edades son: 8, 7, 8, 8, 8, 8, 8, 8, 8 y 9 (años). La media de edad es 8 y la varianza es muy pequeña: 0,22.
Ejemplo 2, una muestra más dispersa; 10 personas en un autobús tienen las siguientes edades: 2, 16, 20, 22, 34, 40, 55, 55, 60, 80. La edad media es 38 y la varianza es 578 (desv. típica 24).
Ejemplo 3, una muestra menos dispersa: 10 personas en un autobús escolar tienen las siguientes edades: 30 (el conductor), 26 (una maestra), 12, 12, 14, 14, 14, 16, 16, 16. En este caso la edad media es 17 y la varianza es 36 (desv. típica 6).
En el primer ejemplo, la media (8) representa con eficacia el valor de la muestra, mientras que en el segundo ejemplo, la media (38) no nos dice mucho sobre la edad de un elemento cualquiera de la muestra. El tercer ejemplo es un caso intermedio.
La regla del 68/95/99.7
En una muestra con una varianza pequeña es más fácil predecir el valor de un elemento desconocido que en una muestra con una varianza mayor. La regla empírica del 68/95/99,7 afirma que, si las distribución de la muestra es normal (un suponer), el 68% de los elementos se encuentran a una distancia de la media menor que el valor de la desviación típica. En el ejemplo 2 podríamos afirmar, con un 68% de fiabilidad, que la edad de uno de los viajeros estaría comprendido entre 14 y 52 (38 +/- 24). En el primer ejemplo este intervalo "de confianza" se reduce a 7,78 - 8,22. Y en el tercer ejemplo el intervalo sería 11-23.
La regla también dice que el 95% de los elementos estaría a una distancia de la media menor de 2 veces la desviación típica (y de 3 veces para el 99,7%).
Cálculo de la varianza
En una muestra continua, una función f(x), la varianza es la integral de la función distancia a la media, teniendo en cuenta el peso de la probabilidad de la función para cada valor de x.
Es más fácil poner la fórmula que explicarlo:

En una muestra discreta (que va a ser siempre nuestro caso cuando evalúemos situaciones que se dan en el poker, donde todos los fenómenos son discretos) la varianza se calcula así:

Como se aprecia a simple vista, el cálculo es el mismo en ambos casos.
Entonces es falso que la varianza no se pueda conocer. Se puede conocer y calcular: sólo hay que aplicar la fórmula ;)
Simulador de varianza para S&G
Ahora vamos a hacer un experimento con el que demostramos que la varianza se puede calcular a priori y, por tanto, se puede actuar sobre sus factores para intentar minimizar su valor.
Repito: vamos a demostrar que un valor que representa la aleatoriedad de un fenónemo es, paradójicamente, predecible.
Imaginemos S&G de 10 jugadores, 3$ de entrada y premios para los tres primeros (15$, 9$ y 6$ respectivamente). Imaginemos, a su vez, que la probabilidad de acabar en cada uno de los puestos es igual (10 puestos, 0,1 en cada puesto).
Con estos datos ya podemos calcular la varianza de estos torneos.
¿cuál es la media? 5,5. Este es el puesto medio en el que deberíamos terminar cada torneo si no hubiese varianza. Es el famoso "medio pollo" de los estadísticos.
¿cuál es la probabilidad de cada uno de los 10 puestos posibles en los que podemos acabar? 1/10= 0,1 (10%).
Aplicamos la fórmula de la varianza: (10-5,5)*(10-5,5)*0,1 + (9-5,5)*(9-5,5)*0,1 ..... = 8,25
Es decir, la varianza de estos torneos es 8,25 (y su desviación típica 2,87).
Ya sabéis, en el 68% de los torneos vamos a acabar entre el puesto 2,7 y el puesto 8,3.
Pues bien, ahora simulamos que tenemos un saldo inicial de 100$ y vamos a jugar 10.000 torneos, calculando el resultado de cada torneo con una función aleatoria (el RNG del excel).
Efectivamente, la varianza de jugar 10.000 torneos es, aproximademente 8,25. Es decir, la varianza de un suceso se puede calcular a priori y coincide con la varianza del resultado del suceso después de suficientes repeticiones (cqd). Este es el primer paso para poder dominar a la varianza.
En las gráficas que incluyo se ven diferentes resultados de ejecutar el experimento. La línea indica la evolución de nuestra banca, debajo de la gráfica se indican los estadísticos (media y varianza) de dos variables:
- el saldo de nuestra banca a la izquierda
- la ganancia de cada partida a la derecha
Como se puede comprobar, la varianza del resultado de cada partida coincide aproximadamente con el valor teórico que hemos calculado (8,25). Sin embargo, el resultado final en forma de saldo es diferente en cada caso.
Otro día hablaremos del riesgo de ruina (Risk of ruin) pero ya podemos adelantar que, como el EV del experimento es 0, el riesgo de ruina es 1 (100%): en este escenario es seguro (100%) que acabaríamos arruinados después de infinitos torneos. De hecho en los ejemplos que hemos incluido alcanzamos la ruina en todos los casos (saldo=0) excepto en uno de ellos.
Esto no quiere decir que este ejemplo sea ganador, sino que no llega a la bancarrota en las 10.000 primeras partidas pero se puede afirmar que llegará.





En resumen, la varianza no es incontrolable: se puede calcular y, por tanto, se puede intentar minimizar su efecto. El peor efecto de la varianza es su relación con la "bancarrota". En próximos artículos analizaremos matemáticamente cómo calcular la probabilidad de acabar en "bancarrota" y, por supuesto, cómo minimizar esta probabilidad.
Fuente de las fórmulas: wikipedia
La puta varianza!
La varianza es el nombre técnico que dan los jugadores de poker a una racha de mala suerte. La varianza justifica que aunque un jugador esté jugando bien esté, a su vez, perdiendo: todas sus acciones tienen EV positivo pero su banca registra pérdidas. Los jugadores dicen (decimos) que no importa perder porque "ha sido culpa de la varianza". El buen jugador de poker parece que sólo tiene un enemigo: la varianza.
Para defenderse de la varianza lo más común es mejorar la gestión de los recursos propios (banca) para que "un zarpazo de la varianza" no termine en "bancarrota". Es decir que una racha negativa no acabe con toda nuestra banca y podamos seguir jugando hasta que llegue una racha positiva.
Mi opinión:
la varianza existe (sin duda) pero no es la única culpable de nuestras perdidas. Además de la varianza, existen otros "culpables" como, por ejemplo, nuestros rivales que son cada vez más y mejores. Y más peligroso que la varianza estadística (aleatoria) es la inestabilidad del nivel de juego propio. Contra la varianza: jugar cada vez mejor y, a ser posible, mejor que los rivales.
Bueno, después del inciso, vamos a explicar qué es la varianza y cómo se calcula. Luego presentaremos unas simulaciones donde intentamos demostrar que la varianza, paradójicamente, siempre tienda a cumplirse.
Definición de varianza
La varianza es el cuadrado de la desviación típica, es decir hay una relación directa entre ambas. Yo siempre usé "desviación típica" pero es más sonoro "varianza" y es el término que se usa normalmente en los foros, artículos y libros de poker.
La varianza mide la dispersión de una muestra en función de la diferencia (la distancia) de cada uno de los elementos de la muestra con el valor medio de la misma.
En un caso extremo, si la varianza es nula (0) todos los elementos de la muestra tienen el mismo valor que coincide con el valor medio de la misma. Si tengo 10 sacos que pesan 25 kg cada uno {25, 25, 25, 25, 25, 25, 25, 25, 25, 25}: el peso medio es 25 y la varianza de la muestra es 0.
Otros ejemplos
Ejemplo 1: en una clase hay 10 niños cuyas edades son: 8, 7, 8, 8, 8, 8, 8, 8, 8 y 9 (años). La media de edad es 8 y la varianza es muy pequeña: 0,22.
Ejemplo 2, una muestra más dispersa; 10 personas en un autobús tienen las siguientes edades: 2, 16, 20, 22, 34, 40, 55, 55, 60, 80. La edad media es 38 y la varianza es 578 (desv. típica 24).
Ejemplo 3, una muestra menos dispersa: 10 personas en un autobús escolar tienen las siguientes edades: 30 (el conductor), 26 (una maestra), 12, 12, 14, 14, 14, 16, 16, 16. En este caso la edad media es 17 y la varianza es 36 (desv. típica 6).
En el primer ejemplo, la media (8) representa con eficacia el valor de la muestra, mientras que en el segundo ejemplo, la media (38) no nos dice mucho sobre la edad de un elemento cualquiera de la muestra. El tercer ejemplo es un caso intermedio.
La regla del 68/95/99.7
En una muestra con una varianza pequeña es más fácil predecir el valor de un elemento desconocido que en una muestra con una varianza mayor. La regla empírica del 68/95/99,7 afirma que, si las distribución de la muestra es normal (un suponer), el 68% de los elementos se encuentran a una distancia de la media menor que el valor de la desviación típica. En el ejemplo 2 podríamos afirmar, con un 68% de fiabilidad, que la edad de uno de los viajeros estaría comprendido entre 14 y 52 (38 +/- 24). En el primer ejemplo este intervalo "de confianza" se reduce a 7,78 - 8,22. Y en el tercer ejemplo el intervalo sería 11-23.
La regla también dice que el 95% de los elementos estaría a una distancia de la media menor de 2 veces la desviación típica (y de 3 veces para el 99,7%).
Cálculo de la varianza
En una muestra continua, una función f(x), la varianza es la integral de la función distancia a la media, teniendo en cuenta el peso de la probabilidad de la función para cada valor de x.
Es más fácil poner la fórmula que explicarlo:

En una muestra discreta (que va a ser siempre nuestro caso cuando evalúemos situaciones que se dan en el poker, donde todos los fenómenos son discretos) la varianza se calcula así:

Como se aprecia a simple vista, el cálculo es el mismo en ambos casos.
Entonces es falso que la varianza no se pueda conocer. Se puede conocer y calcular: sólo hay que aplicar la fórmula ;)
Simulador de varianza para S&G
Ahora vamos a hacer un experimento con el que demostramos que la varianza se puede calcular a priori y, por tanto, se puede actuar sobre sus factores para intentar minimizar su valor.
Repito: vamos a demostrar que un valor que representa la aleatoriedad de un fenónemo es, paradójicamente, predecible.
Imaginemos S&G de 10 jugadores, 3$ de entrada y premios para los tres primeros (15$, 9$ y 6$ respectivamente). Imaginemos, a su vez, que la probabilidad de acabar en cada uno de los puestos es igual (10 puestos, 0,1 en cada puesto).
Con estos datos ya podemos calcular la varianza de estos torneos.
¿cuál es la media? 5,5. Este es el puesto medio en el que deberíamos terminar cada torneo si no hubiese varianza. Es el famoso "medio pollo" de los estadísticos.
¿cuál es la probabilidad de cada uno de los 10 puestos posibles en los que podemos acabar? 1/10= 0,1 (10%).
Aplicamos la fórmula de la varianza: (10-5,5)*(10-5,5)*0,1 + (9-5,5)*(9-5,5)*0,1 ..... = 8,25
Es decir, la varianza de estos torneos es 8,25 (y su desviación típica 2,87).
Ya sabéis, en el 68% de los torneos vamos a acabar entre el puesto 2,7 y el puesto 8,3.
Pues bien, ahora simulamos que tenemos un saldo inicial de 100$ y vamos a jugar 10.000 torneos, calculando el resultado de cada torneo con una función aleatoria (el RNG del excel).
Efectivamente, la varianza de jugar 10.000 torneos es, aproximademente 8,25. Es decir, la varianza de un suceso se puede calcular a priori y coincide con la varianza del resultado del suceso después de suficientes repeticiones (cqd). Este es el primer paso para poder dominar a la varianza.
En las gráficas que incluyo se ven diferentes resultados de ejecutar el experimento. La línea indica la evolución de nuestra banca, debajo de la gráfica se indican los estadísticos (media y varianza) de dos variables:
- el saldo de nuestra banca a la izquierda
- la ganancia de cada partida a la derecha
Como se puede comprobar, la varianza del resultado de cada partida coincide aproximadamente con el valor teórico que hemos calculado (8,25). Sin embargo, el resultado final en forma de saldo es diferente en cada caso.
Otro día hablaremos del riesgo de ruina (Risk of ruin) pero ya podemos adelantar que, como el EV del experimento es 0, el riesgo de ruina es 1 (100%): en este escenario es seguro (100%) que acabaríamos arruinados después de infinitos torneos. De hecho en los ejemplos que hemos incluido alcanzamos la ruina en todos los casos (saldo=0) excepto en uno de ellos.
Esto no quiere decir que este ejemplo sea ganador, sino que no llega a la bancarrota en las 10.000 primeras partidas pero se puede afirmar que llegará.





En resumen, la varianza no es incontrolable: se puede calcular y, por tanto, se puede intentar minimizar su efecto. El peor efecto de la varianza es su relación con la "bancarrota". En próximos artículos analizaremos matemáticamente cómo calcular la probabilidad de acabar en "bancarrota" y, por supuesto, cómo minimizar esta probabilidad.
Fuente de las fórmulas: wikipedia
Riverazo (rectificación)
Riverazo (definición libre): dícese del river que da la vuelta a la mano y hace ganador al jugador que menos expectativas tenía de ganar la mano.
Ahora la jugada del sábado pasado (sólo tengo esta captura de pantalla porque estaba jugando con el portátil de Labot):

Pues eso, S&G DoN de 5$. Tercera mano. Isabella en BB y el rival en SB.
Tres corazones en el flop. Tengo que es el corazón más alto que queda por salir excepto la Q.
que es el corazón más alto que queda por salir excepto la Q.
Ayer escribí:
Aguanto las subidas quedándome, en realidad, comprometido.
El turn le da un trío al rival. El river le da Full y a mí me da una escalera de color al as de corazones preciosa.
Pero después de revisar la mano y comentarla en Poker red me di cuenta que la realidad no fue exactamente así.
Hoy rectifico y pongo la mano entera como prueba:
La cosa fue como sigue:
pre-flop: dos limpers hasta mi BB. check
flop: tres corazones altos en la mesa, proyecto de color. bet 60. uno se tira y el SB lo ve.
turn: se dobla la K. El SB hace "check to the raiser" (yo mismo). bet 200. SB, que tiene un trío de K, ve la apuesta (calling station)
river: Qh. Full para el SB y escalera real para mí. SB hace shove. Insta-call. 1580 fichas al bote.
No Limit Holdem Tournament
$5.00+$0.20
10 players
Converted at weaktight.com
Stacks:
Blinds: 10/20
Pre-flop: (30, 10 players) Hero is BB


4 folds, strelle74 calls 20, 3 folds, janiz104 calls 10, Hero checks
Main Pot (60)
Flop:

 (69, 3 players)
(69, 3 players)
janiz104 checks, Hero bets 60, strelle74 calls 60, janiz104 calls 60
Main Pot (240)
Turn: (249, 3 players)
(249, 3 players)
janiz104 checks, Hero bets 200, strelle74 folds, janiz104 calls 200
River: (649, 2 players)
(649, 2 players)
janiz104 goes all-in 1,230, Hero goes all-in 1,220
Final Pot: 3,080
janiz104 shows:

Hero shows:

janiz104 wins 10 ( lost -1,500 )
Hero wins 3,080 ( won +1,580 )
strelle74 lost -80
Ahora la jugada del sábado pasado (sólo tengo esta captura de pantalla porque estaba jugando con el portátil de Labot):

Pues eso, S&G DoN de 5$. Tercera mano. Isabella en BB y el rival en SB.
Tres corazones en el flop. Tengo
 que es el corazón más alto que queda por salir excepto la Q.
que es el corazón más alto que queda por salir excepto la Q.Ayer escribí:
Aguanto las subidas quedándome, en realidad, comprometido.
El turn le da un trío al rival. El river le da Full y a mí me da una escalera de color al as de corazones preciosa.
Pero después de revisar la mano y comentarla en Poker red me di cuenta que la realidad no fue exactamente así.
Hoy rectifico y pongo la mano entera como prueba:
La cosa fue como sigue:
pre-flop: dos limpers hasta mi BB. check
flop: tres corazones altos en la mesa, proyecto de color. bet 60. uno se tira y el SB lo ve.
turn: se dobla la K. El SB hace "check to the raiser" (yo mismo). bet 200. SB, que tiene un trío de K, ve la apuesta (calling station)
river: Qh. Full para el SB y escalera real para mí. SB hace shove. Insta-call. 1580 fichas al bote.
No Limit Holdem Tournament
$5.00+$0.20
10 players
Converted at weaktight.com
Stacks:
| UTG | garyL237 | (1480) | |
| UTG+1 | m0j0j0j023 | (1500) | |
| UTG+2 | Thomasino999 | (1500) | |
| MP1 | 13gandhi13 | (1550) | |
| MP2 | strelle74 | (1500) | |
| MP3 | Chelyabinsk7 | (1500) | |
| CO | J. Kimberley | (1490) | |
| BTN | TheEnclave | (1470) | |
| SB | janiz104 | (1510) | |
| BB | Hero | (1500) |
Blinds: 10/20
Pre-flop: (30, 10 players) Hero is BB


4 folds, strelle74 calls 20, 3 folds, janiz104 calls 10, Hero checks
Main Pot (60)
Flop:


 (69, 3 players)
(69, 3 players)janiz104 checks, Hero bets 60, strelle74 calls 60, janiz104 calls 60
Main Pot (240)
Turn:
 (249, 3 players)
(249, 3 players)janiz104 checks, Hero bets 200, strelle74 folds, janiz104 calls 200
River:
 (649, 2 players)
(649, 2 players)janiz104 goes all-in 1,230, Hero goes all-in 1,220
Final Pot: 3,080
janiz104 shows:


Hero shows:


janiz104 wins 10 ( lost -1,500 )
Hero wins 3,080 ( won +1,580 )
strelle74 lost -80
Suscribirse a:
Comentarios (Atom)



